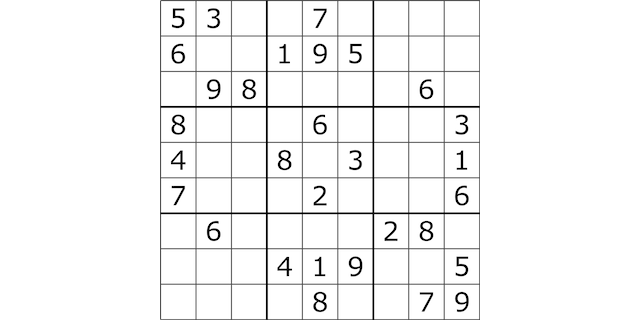
Sudoku is a logic-based, combinatorial number-placement puzzle. The objective is to fill a 9×9 grid with digits so that each column, each row, and each of the nine 3×3 sub-grids that compose the grid contain all of the digits from 1 to 9. The rule of the game is that you can not use the same number more then once in a given row or column.
To help us solve the puzzle in the above image we will put the numbers or the lack of it into a list of list or a 2D array, like so. As a side note, we pre-fill the empty fields we have in the puzzle with zeros.
grid [[5,3,0,0,7,0,0,0,0],
[6,0,0,1,9,5,0,0,0],
[0,9,8,0,0,0,0,6,0],
[8,0,0,0,6,0,0,0,3],
[4,0,0,8,0,3,0,0,1],
[7,0,0,0,2,0,0,0,6],
[0,6,0,0,0,0,2,8,0],
[0,0,0,4,1,9,0,0,5],
[0,0,0,0,8,0,0,7,9]]
And to helps us to a bit with the readability of the matrix we are going to utilize a package call numpy, which prints the matrix as we have above:
import numpy as np
print(np.matrix(grid))
To solve the puzzle we are going to use recursion. But first we need to write a helper function to check if it is actually possible to add a given number into a cell.
def possible(y, x, n):
global grid
# Check if a given number could be added in the row
for i in range(0, 9):
if grid[y][i] == n:
return False
# Check if a given number could be added in the column
for i in range(0, 9):
if grid[i][x] == n:
return False
# Then we check if we can add a given number into the sub-grid (square)
x0 = (x // 3) * 3
y0 = (y // 3) * 3
for i in range(0, 3):
for j in range(0, 3):
if grid[y0 + i][x0 + j] == n:
return False
return True
Now to actually solve the puzzle we iterate over the grid using recursion and backtracking.
def solve():
global grid
for y in range(9):
for x in range(9):
if grid[y][x] == 0:
for n in range(1, 10):
if possible(y, x, n):
grid[y][x] = n
solve() # Here we enter into our recursion
grid[y][x] = 0 # And if we got a bad solution we backtrack.
return # We end up in a dead end we return
# Print solution
print(np.matrix(grid))
# We can use the follow "trick" to re-run the code to find more solutions
input("Solve again?")