Because I got asked that question in interviews now several times, I figured I will write it down here.

What is a scalar product / dot product?

While there is only one way to multiply two numbers, there are two - essentially different – ways in which vectors can be multiplied together. The first one is termed scalar product of vectors, because the result is a scalar number. Or alternatively the dot product because of the dot notation that is used.

In computer graphics we use this product as a way to find the angle between two vectors, and also to show when two vectors are perpendicular.

Definition

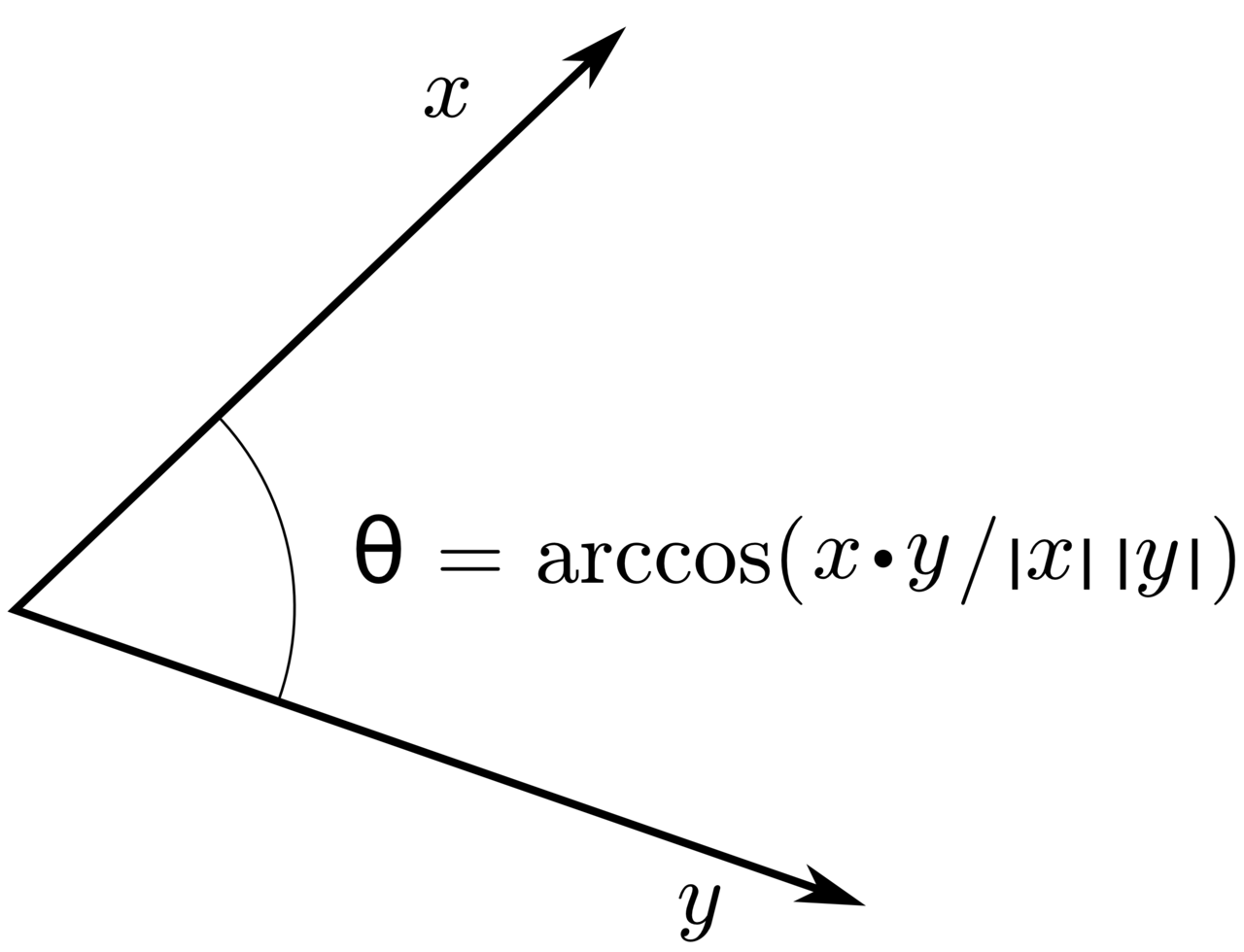
The general definition of the dot product of two vectors involves the modulus¹ of each vector and the angle between the directions of the vectors. If the angle between the two vectors a and b is $\theta$, where $0 \leq \theta \leq 180^{\circ}$, then we define their dot product by

It is crucial to notice that when $a \cdot b$ is calculated, the result is a pure (scalar) number, and not a vector. Because the quantities involved, $\vert a \vert $, $\vert b \vert$, and $ cos \theta $, are each scalar numbers. From the definition we can obtain the formula that is used to calculate the angle between two vectors; it is

In python we can use numpy and write it as follows:

import numpy as np

a = np.array([1, 2, 3])
b = np.array([1, 2, 3])

np.dot(a, b)  # 14

# Alternatively we can write:
a.dot(b)  # 14

Note: We could use the @ operator here, which is actually used in matrix multiplication. And we need to be aware about the matrices size (ndarray should always be dim compatible).

import numpy as np

a = np.array([1, 2, 3])
a.shape  # (3,)

b = np.array([[1, 2, 3]])
b.shape  # (1, 3)

a@b
# Traceback (most recent call last):
#   File "<input>", line 1, in <module>
# ValueError: shapes (3,) and (1,3) not aligned: 3 (dim 0) != 1 (dim 0)

# To fixed that issue we can do the following (transpose b):
a@b.T  # array([14])

Footnotes