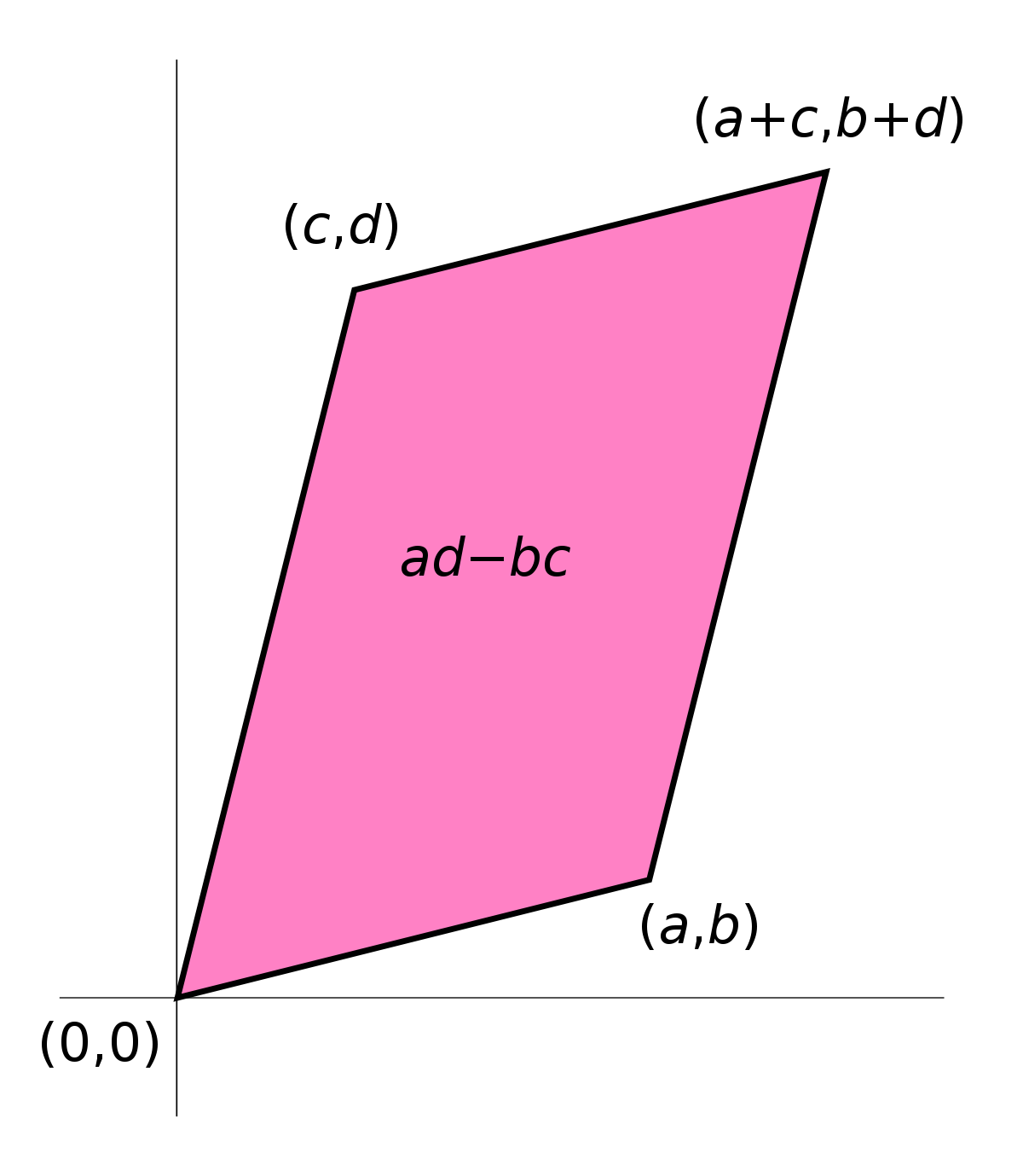
The determinant is a scalar value that can be calculated from the elements of a square matrix and encodes specific properties of the linear transformation described by the matrix.
\[det A = det\begin{bmatrix}a & b \\ c & d \end{bmatrix} = ad - bc\]Some of the properties of determinants are, here are just a few:
- The determinant is equal to the transpose of a matrix - $\vert Xt \vert=X $ For example, if $\vert A \vert = 2$ then the transpose matrix for the same will be $\vert At \vert= -2$
- If a matrix consists of two equal lines with equal values, the resulting matrix is always zero ($\vert X \vert= 0 $).
- $\vert A^{-1} \vert = 1/A$
- The determinants of AB is equal to the product of the individual determinants ($\vert AB \vert= \vert A \vert. \vert B \vert $).
import numpy as np
M = np.array([[1, 2], [3, 4]])
M_det = np.linalg.det(M)