If you want to deep dive into machine learning and especially deep learning, it is vital to have a solid understanding of linear algebra. In the following handful posts or so to come, I hope to help build a good foundation, starting with a brief description of the different data types.

Scalars, Vectors, Matrixes and Tensors

Scalars are single numbers, i.e., 2 (integer) or 3.1415 (float), and are a 0th-order rank tensor. Within machine learning, there are various numbers of interest:

• $\mathbb{N}$ represents positive integer numbers
• $\mathbb{Z}$ represents positive, negative numbers including zero.
• $\mathbb{Q}$ represents rational numbers

Vectors are an ordered array (list) of numbers and are a 1st-order rank tensor, also known as vector spaces. The formal representation of a vector space is $n$-dimensional ($\mathbb{R}^n$), in which we can represent, for example, a point in a three-dimensional space (V = [3, 5, 1]).

The primary use for vectors is to represent a direction or a magnitude (weight, length). In machine learning, a vector often represents a feature with all their components specifying its importance. For example, a vector could represent the relative importance of a word in a given text or the intensity of pixels in an image.

Matrix: is defined by $m x n$ numbers as a rectangular array, where $m$ defines the number of rows and $n$ the number of columns. In other words, the matrix lives in an $mxn$-dimensional vector space, meaning that matrices are vectors that are written in a two-dimensional manner.

In 3D computer graphics, a typical transformation matrix is of $4x4$ dimensions, where different parts in the matrix represent different information, such as “translation,” “scale,” and “rotation”¹ (see image below).

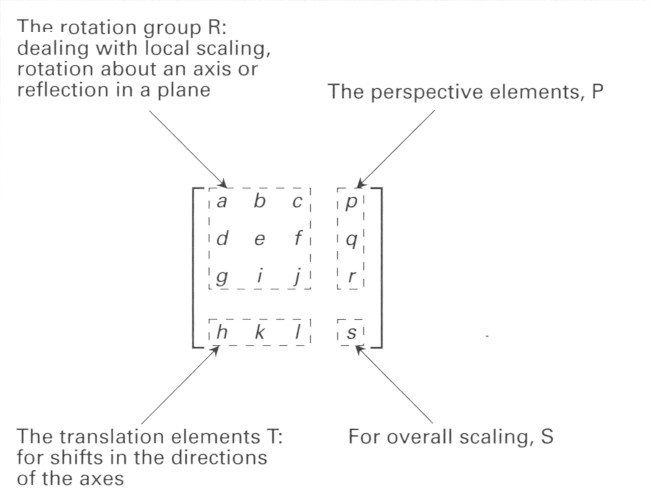
In neural networks, weights are stored as matrices, and feature inputs are stored as vectors.

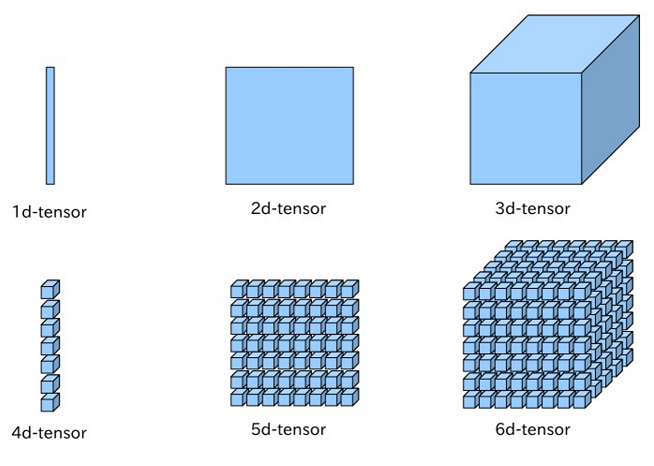
Tensors encapsulates the above-described data types (scalar, vector, and matrix). A tensor has $n$ indices and $m^n$ components, where each index in a tensor ranges over the number of dimensions of space. The notation for a tensor is similar to a matrix (for example, $A=(a_{ij})$, with the exception that a tensor can have an arbitrary number of indices $a_{ijk…}, a^{ijk…}, a_i^{jk}…$, etcetera.¹²

As I alluded above, a tensor is also described in terms of rank. Rank is also known as “order”, “degree”, or “ndims.” For example, a 3rd-order tensor can describe the intensity of multiple channels of an image (RGB) and there is also 4th, 5th and 6th order rank.

Below is the python equivalent representation of the data types using numpy³:

import numpy as np

# Scalar
S = 10

# Vector
V = np.array([1, 2])

# Matrix
M = np.array([[1, 2, 3], [4, 5, 6]])

# Tensor
T = np.array([[[1, 2, 3], [4, 5, 6], [7, 8, 9]],
              [[11, 12, 13], [14, 15, 16], [17, 18, 19]],
              [[21, 22, 23], [24, 25, 26], [27, 28, 29]],
             ])